DFS / BFS

본 글에선 스택과 큐에 대해 알고 있다는 가정하에 설명합니다.

DFS와 BFS는그래프에서 탐색을 하기 위한 알고리즘입니다.

그래프는 아래와 같이 노드와 간선으로 이루어진 구조를 말합니다.

잘 아실 이진트리도 이에 해당합니다.

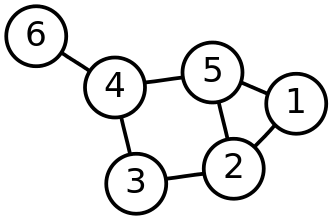
긴말 없이 DFS부터 알아보도록 하겠습니다.

Depth First Search

DFS는 자료구조 stack을 이용해 구현됩니다.

DFS의 작동 과정을 말로 먼저 알아보면

1. 시작 노드를 스택에 삽입하고 방문처리한다.
2. 스택의 최상단 노드에 방문하지 않은 인접 노드를 스택에 삽입하고 방문처리한다.(여러 개일 경우 통상적으로 가장 작은 노드부터 삽입한다.)
3. 방문하지 않은 인접 노드가없을 경우 최상단 노드를 꺼낸다.
4. 방문하지 않은 노드가 없을 때 까지 과정 2,3번을 반복한다.

탐색의 시간 복잡도는 O(N)입니다.

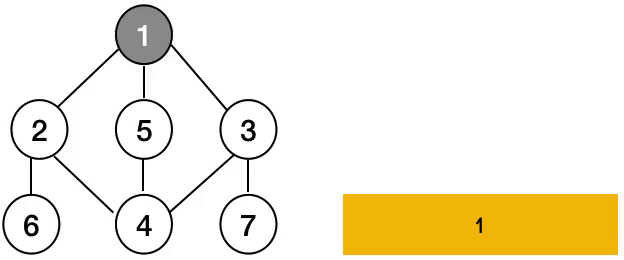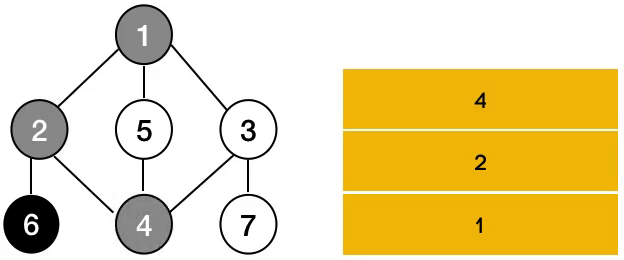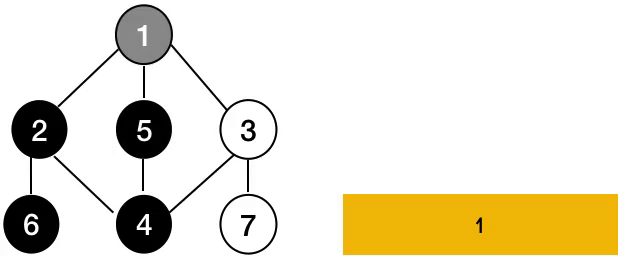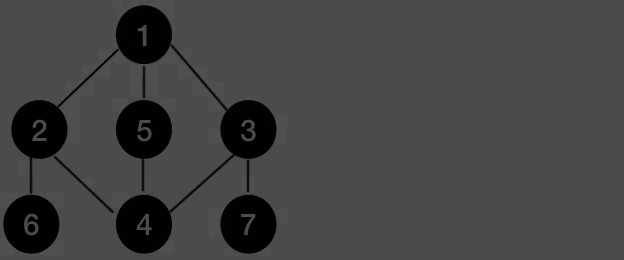
사진으로 알아보면 위와 같습니다.

Breath First Search

BFS는 자료구조 queue를 이용해 구현됩니다.

BFS의 작동 과정을 말로먼저 알아보면

1. 시작 노드를 큐에 삽입하고 방문처리한다.
2. 큐에서 노드를 꺼내고 방문하지 않은 인접노드를 큐에 삽입한다.(여러 개일 경우 통상적으로 노드 크기로 오름차순 하여 삽입한다.)
3. 방문하지 않은 인접노드가 없을 경우 무시한다.
4. 방문하지 않은 노드가 없을 때 까지 과정 2,3번을 반복한다.

탐색의 시간 복잡도는 DFS와 똑같이 O(N)이지만 일반적으로 실제 수행 시간은 DFS보다 좋은 편입니다.

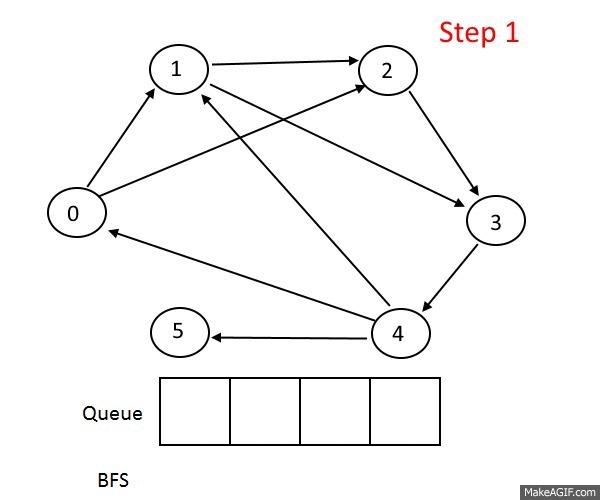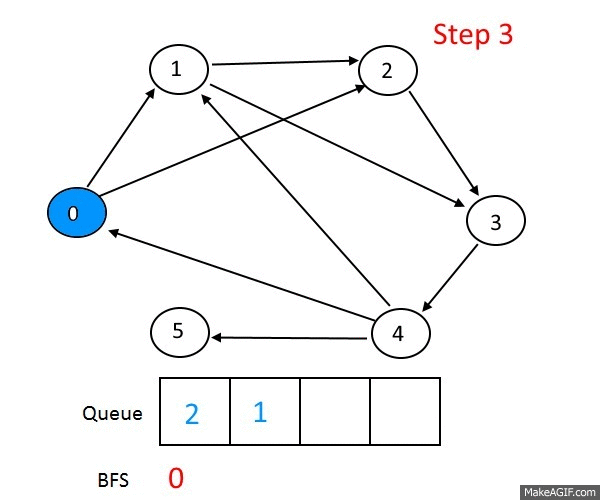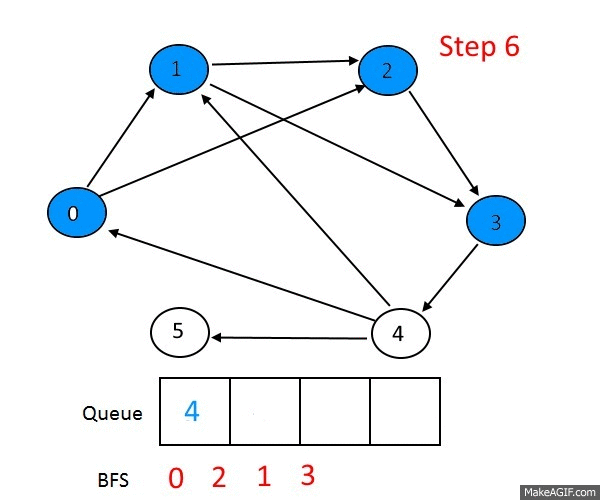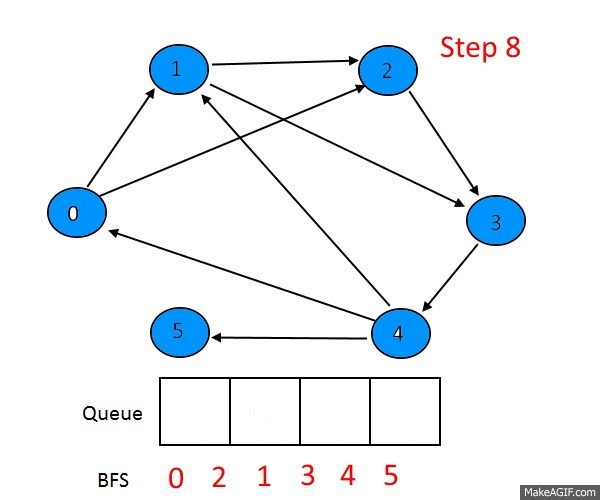
그럼 문제를 같이 하나 풀어보죠

https://school.programmers.co.kr/learn/courses/30/lessons/60063

프로그래머스

from collections import deque

def solution(board):
    n = len(board)
    q = deque([[[1,1],[1,2],0,False]]) # pos(left,up), pos(right,down), cost, is_vertical
    h_visited = [[False] * (n+2) for _ in range(n+2)]
    v_visited = [[False] * (n+2) for _ in range(n+2)]
    board = [[1] * (n+2)] + [[1]+b+[1] for b in board] + [[1] * (n+2)]
    while q:
        state = q.popleft()
        if state[3]:
            if v_visited[state[0][0]][state[0][1]] and v_visited[state[1][0]][state[1][1]]:
                continue
        else:
            if h_visited[state[0][0]][state[0][1]] and h_visited[state[1][0]][state[1][1]]:
                continue
        print(state)
        if [n,n] in state: return state[2]

        if not state[3]:
            h_visited[state[0][0]][state[0][1]] = True
            h_visited[state[1][0]][state[1][1]] = True
            # left
            if board[state[0][0]][state[0][1]-1] == 0 and not h_visited[state[0][0]][state[0][1]-1]:
                q.append([[state[0][0], state[0][1]-1],state[0], state[2]+1, False])
                
            # right
            if board[state[1][0]][state[1][1]+1] == 0 and not h_visited[state[1][0]][state[1][1]+1]:
                q.append([state[1], [state[1][0],state[1][1]+1], state[2]+1, False])
                
            # up
            if board[state[0][0]-1][state[0][1]] == 0 and board[state[1][0]-1][state[1][1]] == 0 and (not h_visited[state[0][0]-1][state[0][1]] or not h_visited[state[1][0]-1][state[1][1]]):
                q.append([[state[0][0]-1,state[0][1]], [state[1][0]-1,state[1][1]], state[2]+1, False])
                
            # down 
            if board[state[0][0]+1][state[0][1]] == 0 and board[state[1][0]+1][state[1][1]] == 0 and (not h_visited[state[0][0]+1][state[0][1]] or not h_visited[state[1][0]+1][state[1][1]]):
                q.append([[state[0][0]+1,state[0][1]], [state[1][0]+1,state[1][1]], state[2]+1, False])
                
            # right to up
            if board[state[0][0]-1][state[0][1]] == 0 and board[state[1][0]-1][state[1][1]] == 0 and not v_visited[state[0][0]-1][state[0][1]] and not v_visited[state[1][0]-1][state[1][1]]:
                q.append([[state[0][0]-1,state[0][1]], state[0], state[2]+1, True])
                
            # right to down
            if board[state[0][0]+1][state[0][1]] == 0 and board[state[1][0]+1][state[1][1]] == 0 and not v_visited[state[0][0]+1][state[0][1]] and not v_visited[state[1][0]+1][state[1][1]]:
                q.append([state[0], [state[0][0]+1,state[0][1]], state[2]+1, True])
                
            # left to up
            if board[state[0][0]-1][state[0][1]] == 0 and board[state[1][0]-1][state[1][1]] == 0 and not v_visited[state[0][0]-1][state[0][1]] and not v_visited[state[1][0]-1][state[1][1]]:
                q.append([[state[1][0]-1,state[1][1]], state[1], state[2]+1, True])
                
            # left to down
            if board[state[0][0]+1][state[0][1]] == 0 and board[state[1][0]+1][state[1][1]] == 0 and not v_visited[state[0][0]+1][state[0][1]] and not v_visited[state[1][0]+1][state[1][1]]:    
                q.append([state[1], [state[1][0]+1,state[1][1]], state[2]+1, True])
                

        if state[3]:
            v_visited[state[0][0]][state[0][1]] = True
            v_visited[state[1][0]][state[1][1]] = True
            # left
            if board[state[0][0]][state[0][1]-1] == 0 and board[state[1][0]][state[1][1]-1] == 0 and (not v_visited[state[0][0]][state[0][1]-1] or not v_visited[state[1][0]][state[1][1]-1]):
                q.append([[state[0][0],state[0][1]-1], [state[1][0],state[1][1]-1], state[2]+1, True])
                
            # right
            if board[state[0][0]][state[0][1]+1] == 0 and board[state[1][0]][state[1][1]+1] == 0 and (not v_visited[state[0][0]][state[0][1]+1] or not v_visited[state[1][0]][state[1][1]+1]):
                q.append([[state[0][0],state[0][1]+1], [state[1][0],state[1][1]+1], state[2]+1, True])
                
            # up 
            if board[state[0][0]-1][state[0][1]] == 0 and not v_visited[state[0][0]-1][state[0][1]]:
                q.append([[state[0][0]-1, state[0][1]],state[0], state[2]+1, True])
                
            # down
            if board[state[1][0]+1][state[1][1]] == 0 and not v_visited[state[1][0]+1][state[1][1]]:
                q.append([state[1], [state[1][0]+1,state[1][1]], state[2]+1, True])
                
            # down to left
            if board[state[0][0]][state[0][1]-1] == 0 and board[state[1][0]][state[1][1]-1] == 0 and not h_visited[state[0][0]][state[0][1]-1] and not h_visited[state[1][0]][state[1][1]-1]:
                q.append([[state[0][0],state[0][1]-1], state[0], state[2]+1, False])
                
            # down to right
            if board[state[0][0]][state[0][1]+1] == 0 and board[state[1][0]][state[1][1]+1] == 0 and not h_visited[state[0][0]][state[0][1]+1] and not h_visited[state[1][0]][state[1][1]+1]:
                q.append([state[0], [state[0][0],state[0][1]+1], state[2]+1, False])
                
            # up to left
            if board[state[0][0]][state[0][1]-1] == 0 and board[state[1][0]][state[1][1]-1] == 0 and not h_visited[state[0][0]][state[0][1]-1] and not h_visited[state[1][0]][state[1][1]-1]:
                q.append([[state[1][0],state[1][1]-1], state[1], state[2]+1, False])
                
            # up to right
            if board[state[0][0]][state[0][1]+1] == 0 and board[state[1][0]][state[1][1]+1] == 0 and not h_visited[state[0][0]][state[0][1]+1] and not h_visited[state[1][0]][state[1][1]+1]:
                q.append([state[1], [state[1][0],state[1][1]+1], state[2]+1, False])

간단히 BFS구현만으로 풀 수 있습니다.

while문에서 제일 처음으로 나오는 if문은 시간 초과를 해결하기 위한 부분입니다.